スマートフォンの傾き角の計算

スマートフォンの水平状態からの傾き角度を計算します。

ここで水平状態とは、例えば、テーブル上にスマートフォンを置いた状態です。

スマートフォンが、水平状態からどの程度傾いているかを計算します。

これが分かると、「水準器」などが作れます。

スマートフォンの座標系

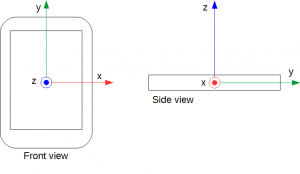
Fig.1 は、スマートフォンの座標系です。

 

Front view

Fig.1 左側は、スマートフォンの正面図（Front view）です。

スマートフォンを正面から見た図です。

• スマートフォンは、画面がある側が「正面」

 

画面中央に座標系の原点があります。

そこから、スマートフォン画面の右方向に「x軸」が伸びています。

また、上方向に「y軸」が伸びています。

「z軸」は、画面から手前方向に伸びています。

 

 

Side view

Fig.1 右側は、スマートフォンの側面図（Side view）です。

スマートフォンを側面から見た図です。

 

 

 

水平状態のスマートフォン

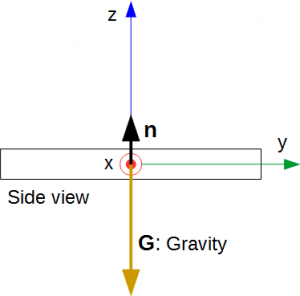
Fig.2 は、水平なテーブルの上に置いたスマートフォンの図です。

• 水平状態： テーブルの上に置いた状態

 

 

Gravity（G）

スマートフォンを水平状態にした場合、重力加速度（G）は Z軸と真逆方向（-Z軸）となります（Fig.2 参照）。

また、重力加速度はスマートフォンの加速度センサーで計測されます。

大体、式(1) の値となります。

 

（注）実際に、スマートフォンをテーブル上に置いて、重力加速度（G）を計測すると、式(1) を中心として値が細かく揺れます。

 

スマートフォン画面の向き（n）

Fig.2 から、z軸がスマートフォン画面の法線ベクトル（n）になっていることが分かります。

• スマートフォンの向き： z軸方向

スマートフォンの向き（n） は、次式となります。

n はz 成分のみの単位ベクトルです。

 

 

傾いたスマートフォン

Fig.3 は、傾いたスマートフォンの図です。

• x軸の回りに、角度（θ）回転して傾いています。

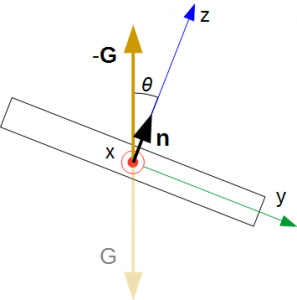
Fig.3 傾いたスマートフォン

この場合、スマートフォンの加速度センサーで検出する重力加速度（G）は次式となります。

（注）記号 | a | は、ベクトル a の絶対値を表します。

 

一般に、スマートフォンの傾き角（θ）は、2 つのベクトル-G とn の内積から求められます（Fig.3 参照）。

ここで、- G は、重力加速度（G）の符号を逆にしたものです（Fig.3 参照）。

 

式(4) を変形すると、次式となります。

n はz 成分のみの単位ベクトルだったので、式(5) は以下となります。

式(6) が、スマートフォンの傾き角（θ）の計算結果です。

ここで、重力加速度（G）は、加速度センサーから得られる値を用います。