水準器アプリの試作1
Contents
スマートフォンからGoogle 検索で「水準器」と検索すると、検索最上位にWebアプリ「水準器」が表示されます。
このWebアプリは、検索画面上で既に動作していて、スマートフォンをテーブルに置くと、テーブルの傾きが計測できます。
今回、このような「水準器」を試作してみました。
試作した「水準器」アプリは、大きく2つの機能で構成されています。
先ず、加速度センサーの値から、スマホの傾斜(方向、大きさ)を計算する、計算機能。
次に、計算結果をビジュアル表示する、表示機能です。
- 計算機能:加速度センサー計算
- 表示機能:スマホ傾斜表示
本記事「水準器アプリの制作1」で、「表示機能」について説明します。
次回の「水準器アプリの制作2」で、「計算機能」について説明します。
水準器アプリの画面
Fig.1 は、スマートフォンの画面を正面からみた図です。
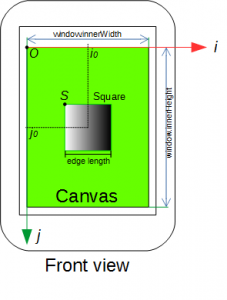
ウィンドウ(Window)上にCanvas があります。
Canvas の幅と高さは次のコマンドで、Windowの幅と高さに合わせています。
canvas.setAttribute(“width”, window.innerWidth); canvas.setAttribute(“height”, window.innerHeight);
window.innerWidth はWindow の幅、window.innerHeight はWindow の高さです(Fig.1 参照)。
そのため、Canvas 座標系は、Window 座標系と完全一致しています(Fig.1 参照)。
- Canvas 座標系: Window 座標系と一致
Canvas 座標系
Canvas 座標の原点(点O)は、Window の左上端の点です。
その点から、右方向にi 軸、下方向にj 軸が伸びています(Fig.1 参照)。
Canvas の中心(点C)
Canvas の中心座標(点Cの座標)は、以下の式で計算します。
C[0] = i0; C[1] = j0;
ここで、C[0] は点C のi 座標、C[1] は点C のj 座標です。
i0, j0 は、Window の中心座標で、以下で与えられます。
i0 = window.innerWidth / 2; j0 = window.innerHeight /2;
正方形(Square)
Canvas 上に、正方形(Square)があります。
正方形の位置とサイズは、以下となります。
- 位 置: Canvas の中心
- サイズ: 一辺が edge length の長さ
正方形の左上に点S があります。
正方形は、グラデーションにより、スマートフォンの傾き方向を表示します。
Fig.1 では、スマートフォンが「右」方向に傾いていることを「表示」しています。
水準器アプリの表示機能
水準器アプリでは、スマートフォンの傾斜(方向、大きさ)を表示します。
正方形(Square)
Fig.2 は、Fig.1 中の正方形(Square)を拡大したものです。
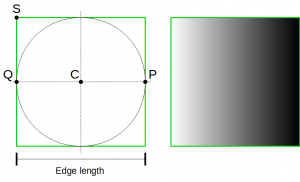
Fig.2 は、傾斜の方向を表示する機能の説明図です。
- 傾斜の方向は、グラデーションで表現します
Fig.2 左側は、グラデーション表示の説明図です。
Fig.2 右側は、グラデーション表示の結果です。
正方形のグラデーション表示(例. 左側:白、右側:黒)で、「右方向に傾いている」ことを表しています。
また、正方形の中心に点Cがあります。
正方形上の点Sの座標は、以下となります。
S[0] = C[0] - edgLen / 2; S[1] = C[1] - edgLen / 2;
ここで、S[0] は点S のi 座標、S[1] は点S のj 座標です。
変数「edgLen」には、正方形の一辺の長さ(Edge length)が代入されています。
グラデーション表示
円
Fig.2 左側、正方形に内接する「円」があります。
点Pと点Qが常に円上にあり、それらは点Cをはさんで対称な位置にあります。
点P・点Qは、スマートフォンの傾き方向が変化することで、円上を移動します。
- 点P・点Qは、円上を動く
傾きの方向
傾きの方向は、加速度センサーの出力から計算します。
「点Cから点Pの方向」に傾いているとして計算し、計算結果は、点Pの円上での位置情報となります。
- 傾きの方向: 点Cから点Pへの方向
グラデーション
点Pと点Qに異なる「色」を指定し、正方形をグラデーション色で描画します。
- 点Pの色: 黒
- 点Qの色: 白
プログラム
プログラム1
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Gradation</title>
<style type="text/css">
* { margin: 0; padding: 0; border: 0; }
</style>
<script>
var canvas;
var ctx;
var i0, j0;
var C = [];
var S = [];
var edgLen = 300; // edge length[pixel]
function drawGradation(P) {
var Q = [];
Q[0] = 2*C[0] - P[0]; // S[0] + (C[0]-S[0]) - (P[0]-C[0])
Q[1] = 2*C[1] - P[1]; // S[1] + (C[1]-S[1]) + (C[1]-P[1])
//
var grad = ctx.createLinearGradient(P[0], P[1], Q[0], Q[1]);
grad.addColorStop(0, "black");
grad.addColorStop(1, "white");
ctx.fillStyle = grad;
//
ctx.fillRect(S[0], S[1], edgLen, edgLen);
ctx.fill();
}
window.onload = function() {
canvas = document.getElementById("canvas");
//
canvas.setAttribute("width", window.innerWidth);
canvas.setAttribute("height", window.innerHeight);
ctx = canvas.getContext("2d");
if (!ctx) return;
//
i0 = window.innerWidth/2;
j0 = window.innerHeight/2;
C[0] = i0;
C[1] = j0;
S[0] = C[0] - edgLen/2;
S[1] = C[1] - edgLen/2;
//
var P = [];
P[0] = S[0] + edgLen; // example
P[1] = S[1] + edgLen/2; //
drawGradation(P);
}
</script>
</head>
<body>
<canvas id="canvas" style="background-color:green;"></canvas>
</body>
</html>
プログラムの解説
グローバル変数
var canvas;
var ctx;
var i0, j0;
var C = [];
var S = [];
var edgLen = 300; // edge length[pixel]
プログラム1 の12 行目では、Window の中心座標を保存する変数(i0, j0)を宣言しています。
13 行目は、点Cの座標を保存するための変数(C)を宣言しています。
14 行目は、点Sの座標を保存するための変数(S)を宣言しています。
15 行目、edgLen は、正方形の一辺の長さを保存する変数で、300(pixel)で初期化しています。
window.onload 関数
window.onload = function() {
canvas = document.getElementById("canvas");
//
canvas.setAttribute("width", window.innerWidth);
canvas.setAttribute("height", window.innerHeight);
ctx = canvas.getContext("2d");
if (!ctx) return;
//
i0 = window.innerWidth/2;
j0 = window.innerHeight/2;
C[0] = i0;
C[1] = j0;
S[0] = C[0] - edgLen/2;
S[1] = C[1] - edgLen/2;
//
var P = [];
P[0] = S[0] + edgLen; // example
P[1] = S[1] + edgLen/2; //
drawGradation(P);
}
プログラム1 の34-35行 で、Canvas の大きさ(横幅、高さ)をWindow の大きさと同じにしています。
39-44 行で、各値(i0, j0, 点C座標, 点S座標)を計算しています。
46-48 行で、点Pの座標値を、一例として、設定しています。
49 行目で、点Pの座標値を実引数として、drawGradation 関数を呼んでいます。
drawGradation 関数
function drawGradation(P) {
var Q = [];
Q[0] = 2*C[0] - P[0]; // S[0] + (C[0]-S[0]) - (P[0]-C[0])
Q[1] = 2*C[1] - P[1]; // S[1] + (C[1]-S[1]) + (C[1]-P[1])
//
var grad = ctx.createLinearGradient(P[0], P[1], Q[0], Q[1]);
grad.addColorStop(0, "black");
grad.addColorStop(1, "white");
ctx.fillStyle = grad;
//
ctx.fillRect(S[0], S[1], edgLen, edgLen);
ctx.fill();
}
プログラム1 の17 行目、drawGradation 関数の仮引数(P)は、点Pの座標が保存されている2 次元配列です。
19-20 行で、点Qの座標を計算しています。
22-25 行で、点Pの座標で「黒」、点Qの座標で「白」となるグラデーションを設定しています。
27 行目で、正方形をグラデーション描画しています。




