数学コンピューター1:比例・反比例1
数学コンピューター(注)を使って、数学を再学習しています。
「比例・反比例」は、数学コンピューター1 の最後の学習項目です。
(注)数学コンピューター
数学問題を解くときに利用するコンピューターの総称
ここでは、次の2 種類の数学コンピューターで計算しています。
- 関 数 電 卓 :fx-375ES-N
- Webサイト:WolframAlpha
数学がとても苦手な人が、数学を学びなおすとき、数学コンピューターが役立ちます。
詳細は、記事「関数電卓で数学を学びなおす」をご参照ください。
変数
変数とは、いろいろな値をとることができる「文字」のことです。
変数として、文字「x」とか「y」を用いることが多いです。
例: 窓開け
幅1.2 m、高さ1.8 m の窓を開ける状況を考えます(Fig.1 参照)。
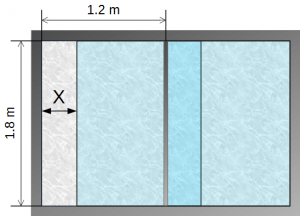
Fig.1 は、窓を少し開けた状態です。
窓を開けた幅(開け幅)を、変数 x としています。
変数 x は、いろいろな値をとることができます。
- 閉まっている :x = 0.0 m
- 少し開いている :x = 0.2 m
- 半分、開いている:x = 0.6 m
- 完全に開いている:x = 1.2 m
変域
変数には必ず、「変域」があります。
変域とは、対応する変数の取り得る範囲のことです。
例:窓開け
Fig.1 の窓開けの場合、変数 x の変域は以下となります。
定数
変数が変域内を変化するのに対して、定数は変化しません。
例:窓開け
窓開けの状況で、窓を開けた幅(開け幅)は変化するので、変数 x としました。
一方、窓の高さ1.8 m や幅1.2 mという値は変化しません(Fig.1 参照)。
よって、窓の高さや幅は定数です。
- 変数:窓を開けた幅(開け幅)
- 定数:窓の高さ・幅
比例
2 つの変数 x と y が次の関係にあるとき、「y は x に比例する」と言います。
ここで、a は定数で、この場合は「比例定数」と言います。
例:窓開け
窓を開けるときの状況を考えます(Fig.2 参照)。
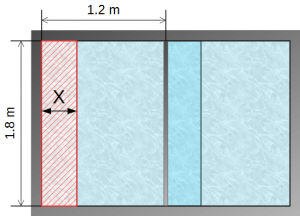
開け幅を x としたとき、窓開け面積(開け面積)を y とします。
このとき、y と x は、次の比例関係にあります。
ここで、a は比例定数で、値は、1.8 m です。
変数 x , y は、いろいろな値をとることができます。
- 閉まっている :x = 0.0 m、y = 1.8×0.0 = 0.00 m^2
- 少し開いている :x = 0.2 m、y = 1.8×0.2 = 0.36 m^2
- 半分、開いている:x = 0.6 m、y = 1.8×0.6 = 1.08 m^2
- 完全に開いている:x = 1.2 m、y = 1.8×1.2 = 2.16 m^2
一方、変数 x, y の値が変化しても、定数の値 1.8 は変化しません。




