JavaScriptプログラム

水準器アプリの試作2

管理者

スマートフォンをテーブルに置くとテーブルの傾きが分かる。

そんな「水準器アプリ」を試作しました。

本記事は、「水準器アプリの試作1」の続き記事です。

 

今回試作する「水準器」は、大きく2つの機能で構成されています。

先ず、加速度センサーから、スマ－トフォンの傾き（方向、角度）を計算する、計算機能。

次に、計算結果をビジュアル表示する、表示機能です。

  • 計算機能：加速度センサー計算
  • 表示機能：スマホ傾き表示

 

前回「水準器アプリの試作1」で、「表示機能」について説明しました。

今回「水準器アプリの試作2」で、「計算機能」について説明します。


 

 

座標系

Fig.1 は、スマートフォンの座標系です。

Fig.1 スマートフォン座標系

 

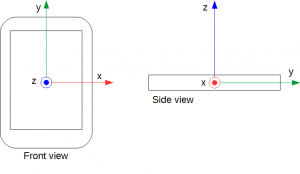
Fig.1 左側が、スマートフォンの正面図です。

Fig.1 右側は、スマートフォンの側面図です。

 

座標系の各軸には色が付いています。

  • x 座標：赤
  • y 座標：緑
  • z 座標：青

 

 

加速度センサー

Fig.2 は、スマートフォンを前傾させた図です。

Fig.2 前傾したスマートフォン

 

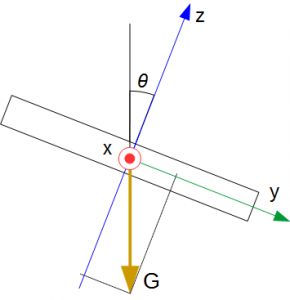
  • スマートフォンを「静かに」前傾させています

そのため、重力（G）以外の加速度が発生していない状態です。

 

Fig.2 の状況で、加速度センサーからの出力値 A は、以下となります（注1）。

（注1）実際には、上記値を中心に、値が細かく振動しています。

傾きの検出

スマートフォンを「静かに」傾けた場合、加速度センサーからの出力値 A は、重力のみを検出します。

重力（G）は、常に鉛直方向を向いているので、重力を検出することで、スマートフォンの傾き（方向、角度）が分かります。

  • 重力（G）を検出　→　スマートフォンの傾きが計算できる

 

 

 

水準器アプリの計算機能

水準器アプリでは、加速度センサーで検出した重力（G） から、スマートフォンの傾き（方向、角度）を計算します。

 

 

傾き方向

スマートフォンの傾き方向の各成分は、以下となります。

傾き角度

スマートフォンの傾き角度は、次式で計算します。

式 (4) の詳細は、以下の記事をご参照ください。

 

 

閾値（Threshold）

傾き角度が小さい場合、傾き角度を「0°」とします。

Fig.2 を見ると、傾き角度が小さくなると、G sin θ の値が小さくなることが分かります。

実際にθ を、1° で計算すると、以下となります（注3）。

（注3）重力加速度（G）の値を、9.8 m/s2 としました

 

そこで、閾値（Threshold）を以下としました。

  • Threshold： 0.15

次の g を計算し、それが Threshold 以下であれば、「0°」とみなしています。

 

 

 

プログラム

プログラム1
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Level</title>
<style type="text/css">
    * { margin: 0; padding: 0; border: 0; }
</style>
<script>
    var canvas;
    var ctx;                    // context
    var i0, j0;                 //
    var C = [];                 // The center of the canvas
    var S = [];                 // Position of the square
    var edgLen    =  300;       // Edge length[pixel]
    var oldTheta  =    0;       // θ
    var oldG_x    =    0;       //
    var oldG_y    =    0;       //
    var THRESHOLD = 0.15;       //
    var osCorrect =    1;       // -1:Android, 1:Others

    window.addEventListener("devicemotion", function(evt){
    //
        var accel = evt.accelerationIncludingGravity;
        var G_x = osCorrect*accel.x;
        var G_y = osCorrect*accel.y;
        var G_z = osCorrect*accel.z;
    //
        var G = Math.sqrt(G_x*G_x+G_y*G_y+G_z*G_z);
        var theta = 180/Math.PI*Math.acos(-G_z/G);
    //
        theta = 0.9*oldTheta + 0.1*theta;
        G_x   = 0.9*oldG_x   + 0.1*G_x;
        G_y   = 0.9*oldG_y   + 0.1*G_y;
        oldTheta = theta;
        oldG_x   = G_x;
        oldG_y   = G_y;
    //
        drawSquare(G_x, G_y);
        writeTheta(theta);
    }, true);

    function writeTheta(theta) {
        ctx.font = "bold 50pt sans-serif";
        ctx.fillStyle = "blue";
        ctx.fillText(theta.toFixed(1).toString(10),C[0]-50,C[1]+20);
    }

	function drawSquare(G_x, G_y) {
        var g = Math.sqrt(G_x*G_x+G_y*G_y);
        if (g>THRESHOLD) {
            var r = edgLen/2;
            var P = [];
            P[0] = S[0] + r + r*G_x/g;
            P[1] = S[1] + r - r*G_y/g;
            drawGradation(P);
        } else {
            ctx.fillStyle = "green";
            ctx.fillRect(S[0], S[1], edgLen, edgLen);
            ctx.fill();
        }
    }

    function drawGradation(P) {
        var Q = [];
        Q[0] = 2*C[0] - P[0];    // S[0] + (C[0]-S[0]) - (P[0]-C[0])
        Q[1] = 2*C[1] - P[1];    // S[1] + (C[1]-S[1]) + (C[1]-P[1])
    //
        var grad = ctx.createLinearGradient(P[0], P[1], Q[0], Q[1]);
        grad.addColorStop(0, "black");
        grad.addColorStop(1, "white");
        ctx.fillStyle = grad;
    //
        ctx.fillRect(S[0], S[1], edgLen, edgLen);
        ctx.fill();        
    }

    window.onload = function() {
        canvas = document.getElementById("canvas");
    //
        canvas.setAttribute("width", window.innerWidth);
        canvas.setAttribute("height", window.innerHeight);
        ctx = canvas.getContext("2d");  
        if (!ctx) return;
    //
        i0 = window.innerWidth/2;
        j0 = window.innerHeight/2;
        C[0] = i0;
        C[1] = j0;
        S[0] = C[0] - edgLen/2;
        S[1] = C[1] - edgLen/2;
    //
        if (navigator.userAgent.match(/Android/)) osCorrect = -1;
    }
</script>
</head>
<body>
    <canvas id="canvas" style="background-color:green;"></canvas>
</body>
</html>

 

プログラム1 の解説

グローバル変数

    var canvas;
    var ctx;                    // context
    var i0, j0;                 //
    var C = [];                 // The center of the canvas
    var S = [];                 // Position of the square
    var edgLen    =  300;       // Edge length[pixel]
    var oldTheta  =    0;       // θ
    var oldG_x    =    0;       //
    var oldG_y    =    0;       //
    var THRESHOLD = 0.15;       //
    var osCorrect =    1;       // -1:Android, 1:Others

プログラム1 の13 行目、2 次元変数 C は、Canvas の中心座標を保存する変数です。

スマートフォンの傾き（方向、角度）は、スマートフォンの中心にある正方形領域に描画します。

14 行目、2 次元変数 S は、その正方形領域のCanvas 上での位置を保存する変数です。

詳細は、記事「水準器アプリの試作1」をご参照ください。

 

15 行目、変数 edgLen は、正方形領域の一辺の長さです。

16 – 18 行、各値を平滑化するための変数です。

  • oldTheta： 傾き角度（θ）
  • oldGx      ：傾き方向（Gx）
  • oldGy      ：傾き方向（Gy)

詳細は、記事「スマホセンサーのノイズ軽減」をご参照ください。

 

19 行目、変数 THRESHOLD は、式 (6) の閾値です。

 

20 行目、変数 osCorrect は、スマートフォンがAndroid の場合、補正するための変数です。

詳細は、記事「加速度センサーのAndroid 補正」をご参照ください。

 

 

window.onload 関数

    window.onload = function() {
        canvas = document.getElementById("canvas");
    //
        canvas.setAttribute("width", window.innerWidth);
        canvas.setAttribute("height", window.innerHeight);
        ctx = canvas.getContext("2d");  
        if (!ctx) return;
    //
        i0 = window.innerWidth/2;
        j0 = window.innerHeight/2;
        C[0] = i0;
        C[1] = j0;
        S[0] = C[0] - edgLen/2;
        S[1] = C[1] - edgLen/2;
    //
        if (navigator.userAgent.match(/Android/)) osCorrect = -1;
    }

プログラム1 の86 – 91 行、詳細は、記事「水準器アプリの試作1」をご参照ください。

 

93 行目、スマートフォンがAndroid の場合、osCorrect に -1 を代入します。

詳細は、記事「加速度センサーのAndroid 補正」をご参照ください。

 

 

devicemotion イベント

    window.addEventListener("devicemotion", function(evt){
    //
        var accel = evt.accelerationIncludingGravity;
        var G_x = osCorrect*accel.x;
        var G_y = osCorrect*accel.y;
        var G_z = osCorrect*accel.z;
    //
        var G = Math.sqrt(G_x*G_x+G_y*G_y+G_z*G_z);
        var theta = 180/Math.PI*Math.acos(-G_z/G);
    //
        theta = 0.9*oldTheta + 0.1*theta;
        G_x   = 0.9*oldG_x   + 0.1*G_x;
        G_y   = 0.9*oldG_y   + 0.1*G_y;
        oldTheta = theta;
        oldG_x   = G_x;
        oldG_y   = G_y;
    //
        drawSquare(G_x, G_y);
        writeTheta(theta);
    }, true);

プログラム1 の24 – 27 行、加速度センサーの値を得ています。

また、スマートフォンがAndroid の場合、補正処理しています。

 

29 – 30 行、傾き角度（θ）を計算しています。

32 – 37 行、各値（θ, Gx, Gy）の平滑化処理しています。

39 行目、drawSquare 関数を呼んでいます。

40 行目、writeTheta 関数を呼んでいます。

 

writeTheta 関数

    function writeTheta(theta) {
        ctx.font = "bold 50pt sans-serif";
        ctx.fillStyle = "blue";
        ctx.fillText(theta.toFixed(1).toString(10),C[0]-50,C[1]+20);
    }

正方形の中心に、傾き角（θ）の値を表示しています。

 

drawSquare 関数

    function drawSquare(G_x, G_y) {
        var g = Math.sqrt(G_x*G_x+G_y*G_y);
        if (g>THRESHOLD) {
            var r = edgLen/2;
            var P = [];
            P[0] = S[0] + r + r*G_x/g;
            P[1] = S[1] + r - r*G_y/g;
            drawGradation(P);
        } else {
            ctx.fillStyle = "green";
            ctx.fillRect(S[0], S[1], edgLen, edgLen);
            ctx.fill();
        }
    }

プログラム1 の50 行目、閾値処理のための変数 g を計算しています。

52 – 56 行、g が閾値より大なので、drawGradation 関数へ渡す引数を計算し、drawGradation 関数を呼んでいます。

58 – 60 行、g が閾値以下なので、正方形を「green」で塗ります。

 

 

drawGradation 関数

    function drawGradation(P) {
        var Q = [];
        Q[0] = 2*C[0] - P[0];    // S[0] + (C[0]-S[0]) - (P[0]-C[0])
        Q[1] = 2*C[1] - P[1];    // S[1] + (C[1]-S[1]) + (C[1]-P[1])
    //
        var grad = ctx.createLinearGradient(P[0], P[1], Q[0], Q[1]);
        grad.addColorStop(0, "black");
        grad.addColorStop(1, "white");
        ctx.fillStyle = grad;
    //
        ctx.fillRect(S[0], S[1], edgLen, edgLen);
        ctx.fill();        
    }

drawGradation 関数は、記事「水準器アプリの試作1」をご参照ください。

 

こちらもおすすめ

chisou_mizu

UnityをGitHubで管理しよう

管理者

GitHubとSourcetreeの学び方

管理者

SVGでタイマーを作る

管理者

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です