数学コンピューター2：式の計算3

数学コンピューター（注）を使って、数学を再学習しています。

数学コンピューター2 では、中学数学2 の内容に準拠しています。

本記事は、記事「数学コンピューター2 ：式の計算2」の続き記事となります。

 

 

（注）数学コンピューター

数学問題を解くときに利用するコンピューターの総称

ここでは、次の2 種類の数学コンピューターで計算しています。

• 関 数 電 卓 ：fx-375ES-N
• Webサイト：WolframAlpha

数学がとても苦手な人が、数学を学びなおすとき、数学コンピューターが役立ちます。

詳細は、記事「関数電卓で数学を学びなおす」をご参照ください。

 

 

前回と前々回記事において、式の計算には「順方向」と「逆方向」があることを述べました。

 

例. 次式の計算を考えます

• 順方向：変数 X に値を代入し、Y を計算する
• 逆方向：変数 Y に値を代入し、X を計算する

 

詳細は、以下の記事をご参照ください。

• 順方向：「数学コンピューター2：式の計算」
• 逆方向：「数学コンピューター2：式の計算2」

 

今回、式の計算（順・逆方向混合）を例示します。

 

 

 

式の計算例（順・逆方向混合）

ここでは、fx-375ES-N を用いる場合、ソルブ機能を使用しました。

 

 

例1.

一辺 A cm の正方形の周りの長さを L 、面積を Sとしたとき、次式が成り立ちます。

 

質問：

30 m のロープがあります。

そのロープを4 等分して（目印を付ける）、地面に正方形を作ります。

正方形の面積はいくらですか？

 

考え方：

上記、正方形の方程式を利用する。

• L：ロープの長さ
• A：正方形の一辺の長さ
• S：正方形の面積

 

計算の方向（順・逆）は以下となります。

• 逆方向：L = 30 m からA を計算
• 順方向：A からS を計算

 

 

計算：

• fx-375ES-N
  • 入力：　Y=4A,A　←　Y=30
  • 回答：　5.641895835　→　[Ans]
  • 入力：　Y=A^2,Y　←　A=[Ans]
  • 回答：　56.25

 

（注）[Ans]ボタン：

fx-375ES-N では、直前の計算結果を保存していて、[Ans]ボタンでそれを呼出せます。

（注）変数 L の代わりに Y を使用しました。

 

 

• WolframAlpha1
  • 入力：　L = 4 A, L = 30
  • Solution:　A = 15/2　→　15/2 をクリック
  • 入力：　S = (15/2)^2
  • Solution：　S = 225/4 = 56.25

 

（注）15/2 をクリック：

Solution の「15/2」 をクリックすると、新しい「入力画面」が、15/2 が入力済みで開きます。

 

 

• WolframAlpha2
  • 入力：　L = 4 A, S = A^2, L = 30
  • Solution:　A = 15/2 = 7.5, S = 225/4 = 56.25

 

（注）L = 4 A, S = A^2

2つの式（L=4A, S=A^2）において、変数A は同じ意味（同じ正方形の一辺の長さ）なので、入力欄に2 つの式を同時に記述できます。

 

 

例2.

半径 R cm の円の円周 L 、面積S は、次式となります。

 

 

質問：

30 m のロープがあります。

そのロープを使い、地面に円を作ります。

円の面積はいくらでしょうか？

 

 

考え方：

上記、円の方程式を利用する。

• L：ロープの長さ
• R：円の半径
• S：円の面積

計算の方向（順・逆）は以下となります。

• 逆方向：L = 30 m からR を計算
• 順方向：R からS を計算

 

 

計算：

• fx-375ES-N
  • 入力：　Y=2πA,A　←　Y=30
  • 回答：　A=4.774648293　→　[Ans]
  • 入力：　Y=πA^2,Y　←　A=[Ans]
  • 回答：　Y=71.61972439

（注）変数L の代わりにY を、変数R の代わりにA を使用しました。

• WolframAlpha1
  • 入力：　L = 2πR, S = πR^2, L = 30
  • Solution:　R = 15/π　→　 15/π をクリック
  • 入力：　S = π(15/π)^2
  • Solution：　225/π = 71.61972439135…

 

• WolframAlpha2
  • 入力：　L = 2πR, S = πR^2, L = 30
  • Solution:　R = 15/π = 4.7746…, S = 225/π = 71.61972439135…

（注）L = 2πR, S = πR^2

2つの式（L = 2πR, S = πR^2）において、変数 R は同じ意味（同じ円の半径）なので、入力欄に2 つの式を同時に記述できます。

 

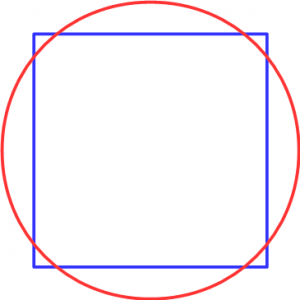
Fig.1 は、周長が同じ正方形と円の図です。

周長が30 m の場合、例.1 と 例.2 の結果より、以下となります。

• 正方形：辺長（7.50 m）、面積（56.25 m^2）
• 　円　：半径（4.77 m）、面積（71.62 m^2）

 

 

 

Question

円柱状（直径3 cm, 高さ6 cm）のカラー粘土があります。

この粘土をこねて、球状にしました。

 

式：

半径がR cm、高さH cm の円柱の体積V は、以下となります。

半径がR cm の球の体積V は、以下となります。

 

質問：

球の大きさ（半径）はどれくらいでしょうか？